题意描述
给出一个8皇后的摆放方式,要求使用最少的移动步数将其移动为合法的摆放方式。 一次移动可以将某个皇后横着、竖着、斜着移动任意距离,但不能越过其他皇后。 合法摆放方式指任意两个皇后不在同一行、同一列、同一对角线。
题意分析
一般的思路是预处理出所有合法摆法(数量很少,共92个),求出当前摆法移动到每个合法摆法的最少步数,取最小值即可。
这个题目的关键就是如何求解当前摆法到一个合法摆法的最少移动步数。题目标程使用方法的是状压DP,也有其他人使用二分图最小匹配等方法。 然而不管使用哪种方法,他们都使用了同样一个结论:将一个皇后移动到目标位置的步数不会受到其他皇后的影响。
关于这个结论,我没有在网络上找到合理的证明方法——后来的事实证明这个结论是错误的。下面我们将从这个结论的反例出发,进行一些思考。
反例与思考
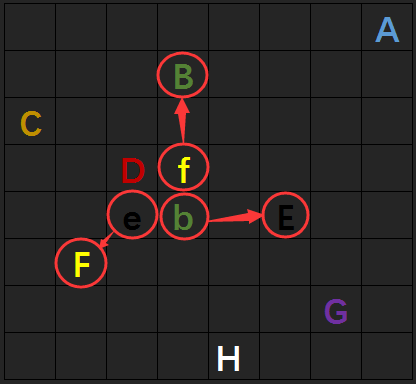
下图展示了上述结论的一个反例。图中的大写字母 A~H 表示一个合法摆法,小写字母 b、e、f 表示当前的摆法(这里只展示了3个皇后)。

这里,b 要移动到位置 B,e 要移动到位置 E,f 要移动到位置 F。因为三个皇后相互之间的阻挡,总共需要4步才能移动到最终的位置。 而如果没有皇后之间的阻挡,只需要3步就可以移动到最终的位置。因此,上述的结论是不正确的。
但是,我们也不能简单地认为题目的标程是错误的。因为我们要找的是最少步数,并不要求每个皇后移动到特定的位置。 比如上面的反例,如果我们采取下图的移动方式,就可以移动更少的步数。
因此,我们只需要证明在获得最少步数的移动方式中,不会出现像第一张图中相互阻挡的情况就行了。
问题是。我并不会证……
15 May 2017