Several Classical Partial Differential Equations: Numerical and Exact Solutions

Yu Zhang

April 2023

Introduction

Numerical solutions of partial differential equations (PDE) are often employed in the field of physical simulations. Numerical methods are used for solving these equations because obtaining exact solutions is usually intricate and often requires specific analyses for each form. To demonstrate the differences between numerical and exact solutions, we present examples of classical PDEs in both forms. For the purpose of visualization, we provide examples in two-dimensional space. All code implementations in this article can be found at Github.

Transport Equation

The transport equation, also known as the advection equation. The transport equation's initial value problem can be formulated as follows: $$ \\ \begin{cases} u_t + \mathbf{b} \cdot Du = 0 & \text{in} \ R^n \times (0, \infty)\\ \quad \quad \quad \quad \ u = g &\text{on} \ R^n \times \{t=0\} \end{cases} $$ Here, $\mathbf{b}$ is a fixed vector in $R^n$, $\mathbf{b} = (\mathbf{b}_1, \cdots, \mathbf{b}_n)$. The function $u:R^n \times [0, \infty) \rightarrow R$ is the function to be solved, denoted as $u=u(\mathbf{x}, t)$. The variable $\mathbf{x} \in R^n$ represents a point in space, and $t \geq 0$ denotes time. $u_t$ is the partial derivative of $u$ with respect to time $t$, and $Du = D_{\mathbf{x}}u = (u_{\mathbf{x}_1}, \cdots, u_{\mathbf{x}_n})$ represents the gradient of $u$ with respect to spatial variable $\mathbf{x}$.

Exact Solution

The analytical solution for the transport equation's initial value problem is given by $$ u(\mathbf{x}, t) = g(\mathbf{x} - \mathbf{b}t),\quad (\mathbf{x} \in R^n, t \geq 0) $$

Numerical Solution

For solving the transport equation, a straightforward numerical method is the forward time-centered space (FTCS) method, a finite difference approach. In two dimensions, using $u^{n}_{i, j}$ to denote the numerical value of function $u$ at grid point $(i, j)$ and time step $\Delta t$ with grid spacing $\Delta x$, the equation becomes $$ \frac{u^{n+1}_{i, j} - u^n_{i, j}}{\Delta t} + \mathbf{b} \cdot (\frac{u^n_{i+1, j}-u^n_{i-1, j}}{2 \Delta x}, \frac{u^n_{i, j+1}-u^n_{i, j-1}}{2 \Delta x}) = 0 $$

Stability Analysis

In practice, the FTCS method is unconditionally unstable. To address this issue, we can replace the central difference scheme in space with an upwind scheme, resulting in a conditionally stable numerical method. Stability analysis of these numerical methods can be found here.

Case Study

We provide a two-dimensional example with the following parameters: $$ \begin{aligned} &\mathbf{b} = (1, 1), \\ &\begin{cases} g(\mathbf{x}) = 1, &|\mathbf{x}| \leq 10 \\ g(\mathbf{x}) = 0, &|\mathbf{x}| > 10 \end{cases} \end{aligned} \\ $$ The function $g$ is chosen for convenience, although not $C^1$ continuous.

The comparison between numerical and exact solutions is shown below:

In the figures, Figure 1 depicts the FTCS method, Figure 2 shows the upwind scheme, and Figure 3 presents the exact solution. From the experimental results, we observe numerical divergence with FTCS, while the upwind scheme maintains stability.

Code

Physical Interpretation

The transport equation describes the change of a physical quantity $u$ at every fixed point in space under the influence of a velocity field, as viewed in an Eulerian perspective. The value of $b$ in the equation corresponds to the velocity of the field. This explains the motion of the circular region in the upper-right direction in the presented case. Additionally, the transport equation can be associated with the material derivative. The material derivative is given by: $$ \frac{Du}{Dt} = \frac{\partial u}{\partial t} + \mathbf{b} \cdot \nabla u $$ Thus, the transport equation describes the evolution of the quantity in response to an external velocity field over time when the material derivative is zero (indicating no change in the physical quantity itself).

Laplace’s Equation

Laplace's equation is a special case of Poisson's equation: $$ \left\{ \begin{eqnarray} \nabla^2 u &=& 0 & &\text{in} \ U\\ u &=& g & &\text{on} \ \partial U \end{eqnarray} \right. $$ Here, $u:\bar{U} \rightarrow R$ is the function to be solved, $u=u(\mathbf{x})$. $U \subset R^n$ is a given open set, and $\nabla^2 u = \sum_{i=1}^n u_{\mathbf{x}_i \mathbf{x}_i}$.

Exact Solution

Several methods can be employed to find the exact solution of Laplace’s equation, such as the Green’s function method or separation of variables. Due to length constraints, we omit the detailed process. An example of solving Laplace’s equation using separation of variables in polar coordinates can be found here.

Numerical Solution

In this section, we present the numerical results of the Laplace equation via the Jacobi iterative method, the Walk-on-spheres method, and the Walk-on-boundary method, respectively.

Jacobi Method

A simple approach is to use the Jacobi iteration method to converge the equation to its solution, where $u^n$ denotes the result of the $n$-th iteration. Utilizing central difference discretization in space for $\nabla^2 u$, we have $$ \nabla u^{n}_{i, j} = \frac{u^n_{i+1, j} + u^n_{i-1, j} + u^n_{i, j+1} + u^n_{i, j-1} - 4u^n_{i, j}}{\Delta x^2} $$ As we want $\nabla u^{n}_{i, j} = 0$, an iterative formula can be derived: $$ \nabla u^{n+1}_{i, j} = \frac{u^n_{i+1, j} + u^n_{i-1, j} + u^n_{i, j+1} + u^n_{i, j-1}}{4} $$

Walk-On-Spheres (WoS) And Walk-On-Boundary (WoB) Methods

A detailed introduction to Wos and WoB can be found on these two websites: WoS and WoB.

Convergence Analysis

Omitted.

Case Study

We use this example as a case study. The Cauchy problem in polar coordinates is described as follows: $$ \begin{cases} \nabla^2 u = 0, & 1 < r < 2 \\ u(r, \theta) = 0, & r = 1 \\ u(r, \theta) = \sin \theta, & r = 2 \end{cases} $$

Jacobi Method

The numerical result of Jacobi method is shown below:

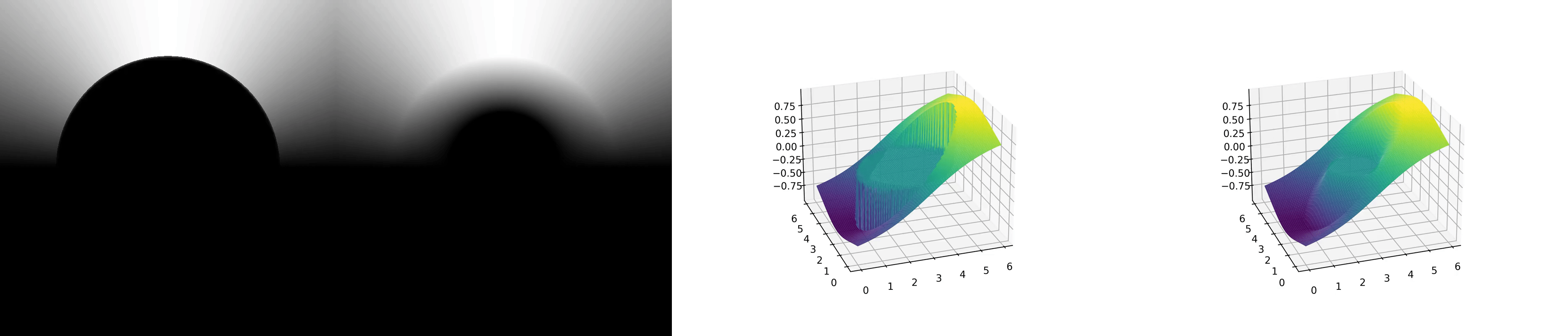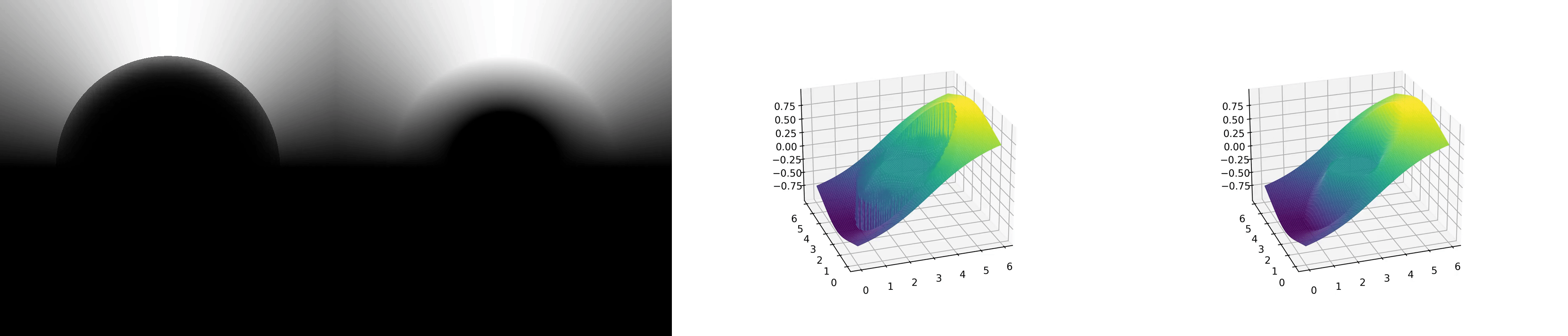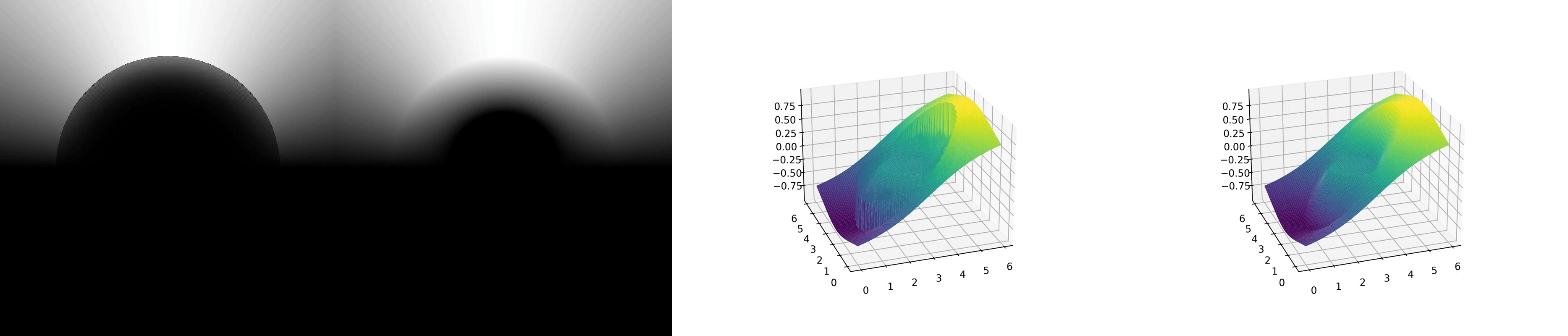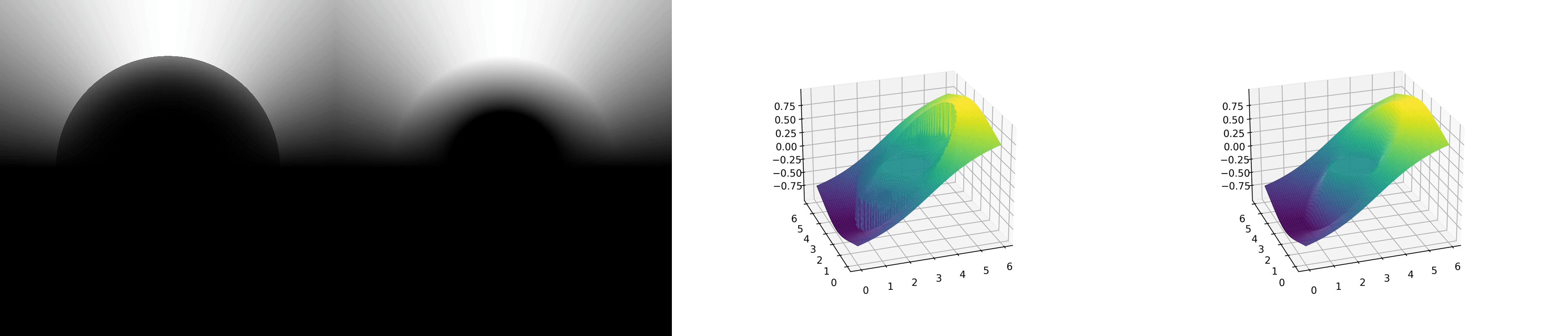
Figures 1 and 3 show the convergence process of the numerical method, while Figures 2 and 4 show the final exact solution.

Code

WoS and WoB

In the implementation of these two methods, we employed the Temporal Accumulation technique to accumulate results from each frame, making it easier to visualize the process of convergence. For WoS, within each frame’s sampling process, for each position in domain, we recursively sample until the sampled points approach the boundary. For WoB, we set the path length per frame to 1, meaning we stop after sampling one point on the boundary. The experimental results are as follows:

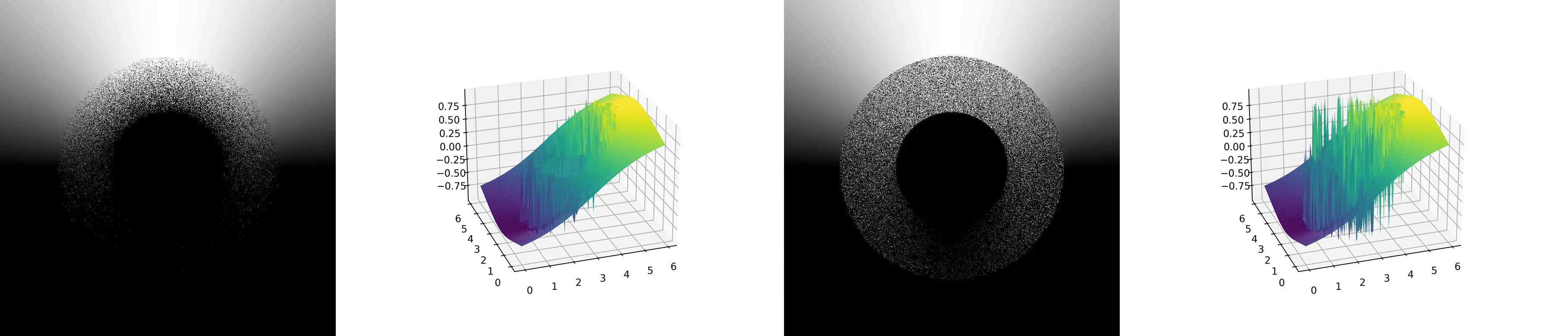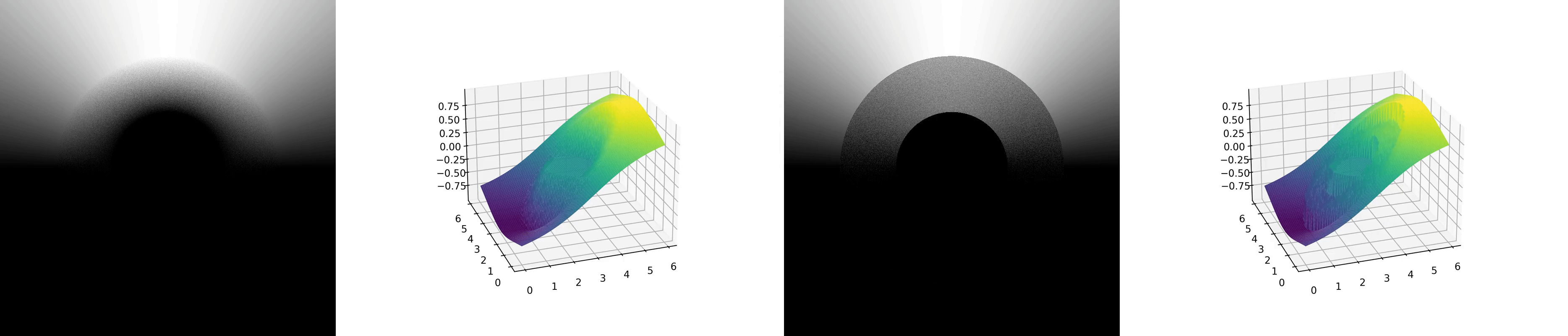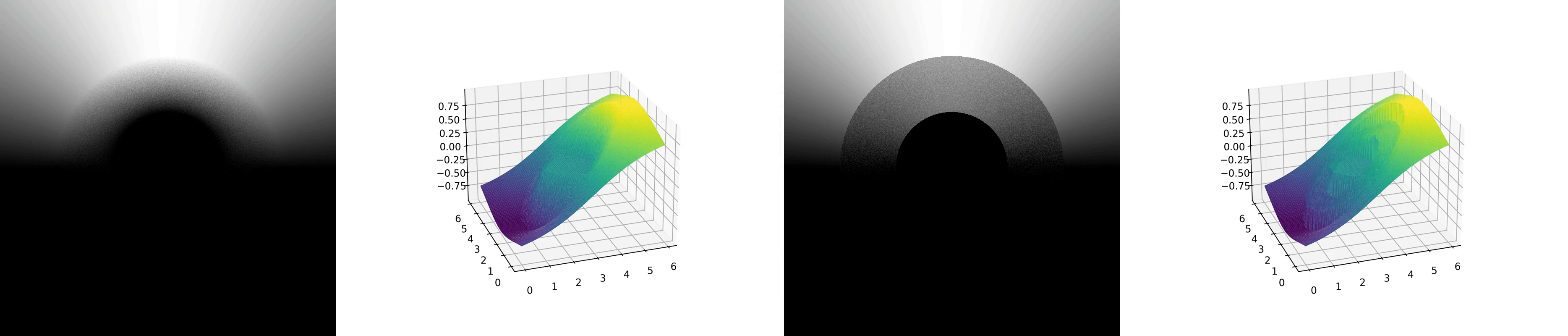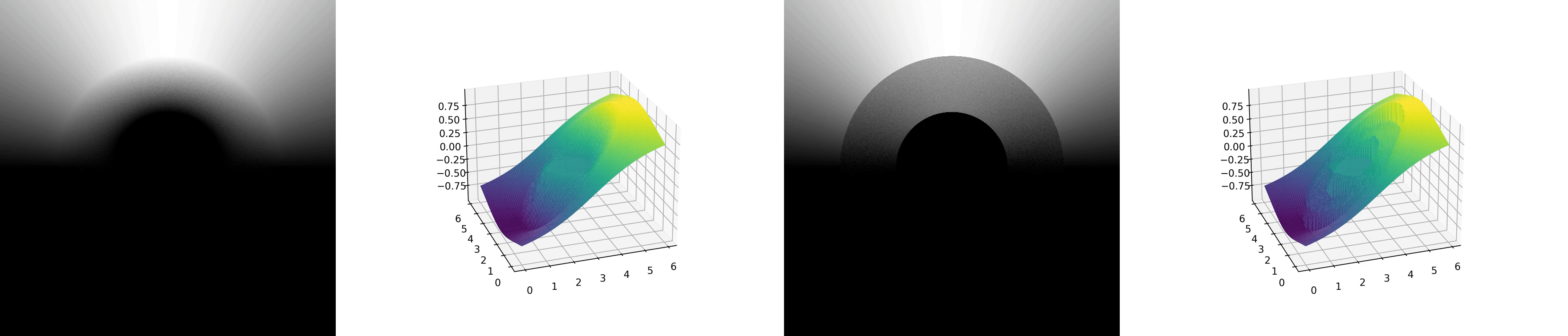
The first two animations show the convergence process of the WoS method, while the latter two show the convergence process of the WoB method.

Code: WoS, WoB

Heat Equation

The heat equation, also known as the diffusion equation, can be formulated as follows: $$ \\ \begin{cases} u_t - \alpha \nabla^2 u = 0 & \text{in} \ R^n \times (0, \infty)\\ \quad \quad \quad \ u = g &\text{on} \ R^n \times \{t=0\} \end{cases} $$

Exact Solution

As before, the exact solution’s form is omitted due to its complexity.

Numerical Solution

Similar to the transport equation, we can use the FTCS method to solve the heat equation. The finite difference form is as follows: $$ \frac{u^{n+1}_{i, j} - u^n_{i, j}}{\Delta t} - \alpha \frac{u^n_{i+1, j} + u^n_{i-1, j} + u^n_{i, j+1} + u^n_{i, j-1} - 4u^n_{i, j}}{\Delta x^2} = 0 $$

Stability Analysis

In this case, the FTCS method is conditionally stable. In two dimensions, the stability condition is $\Delta t < \frac{\Delta x^2}{4}$. The detailed analysis can be found here.

Case Study

A two-dimensional example is provided with the following parameters: $$ \begin{aligned} &\alpha = 1, \\ &\begin{cases} g(\mathbf{x}) = 1, &|\mathbf{x}| \leq 10 \\ g(\mathbf{x}) = 0, &|\mathbf{x}| > 10 \end{cases} \end{aligned} \\ $$ As there is no direct comparison case, we do not show the visualization of the exact solution. The figure below illustrates the numerical solution's evolution over time.

Code

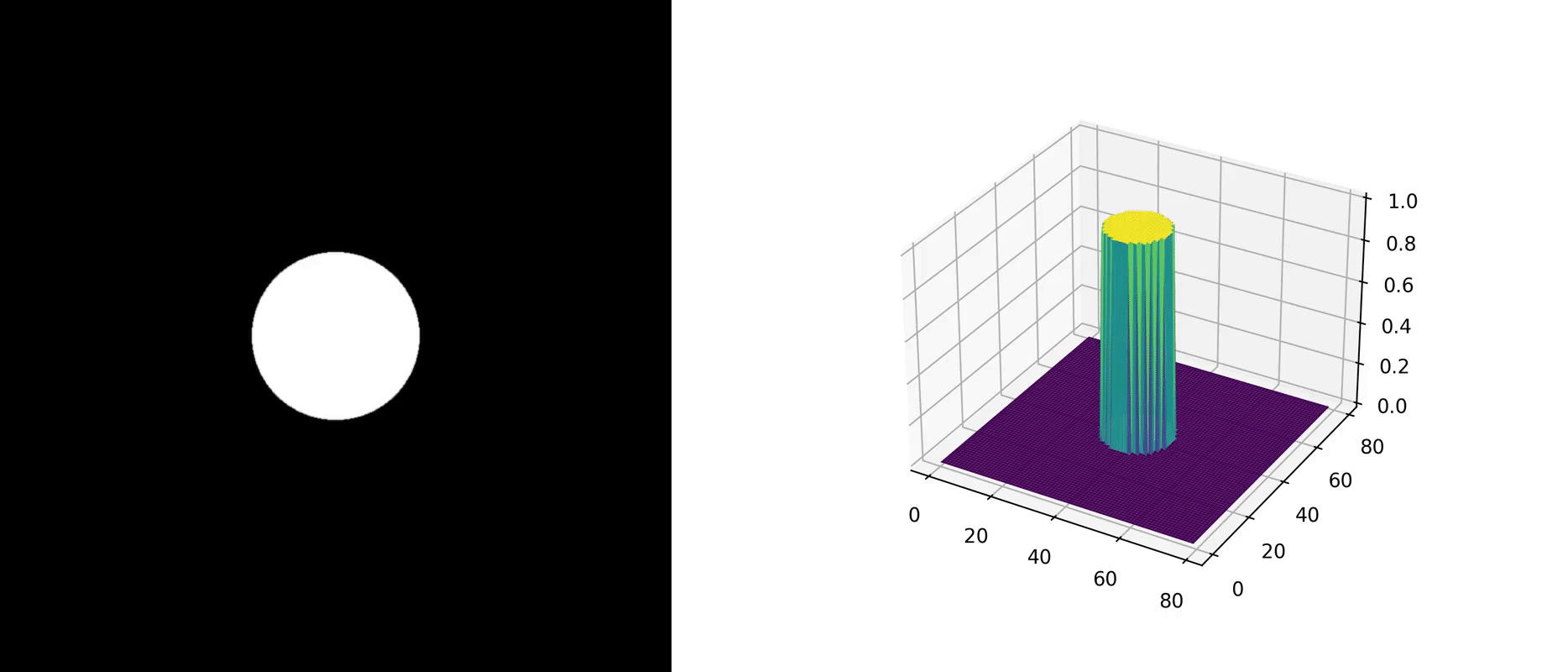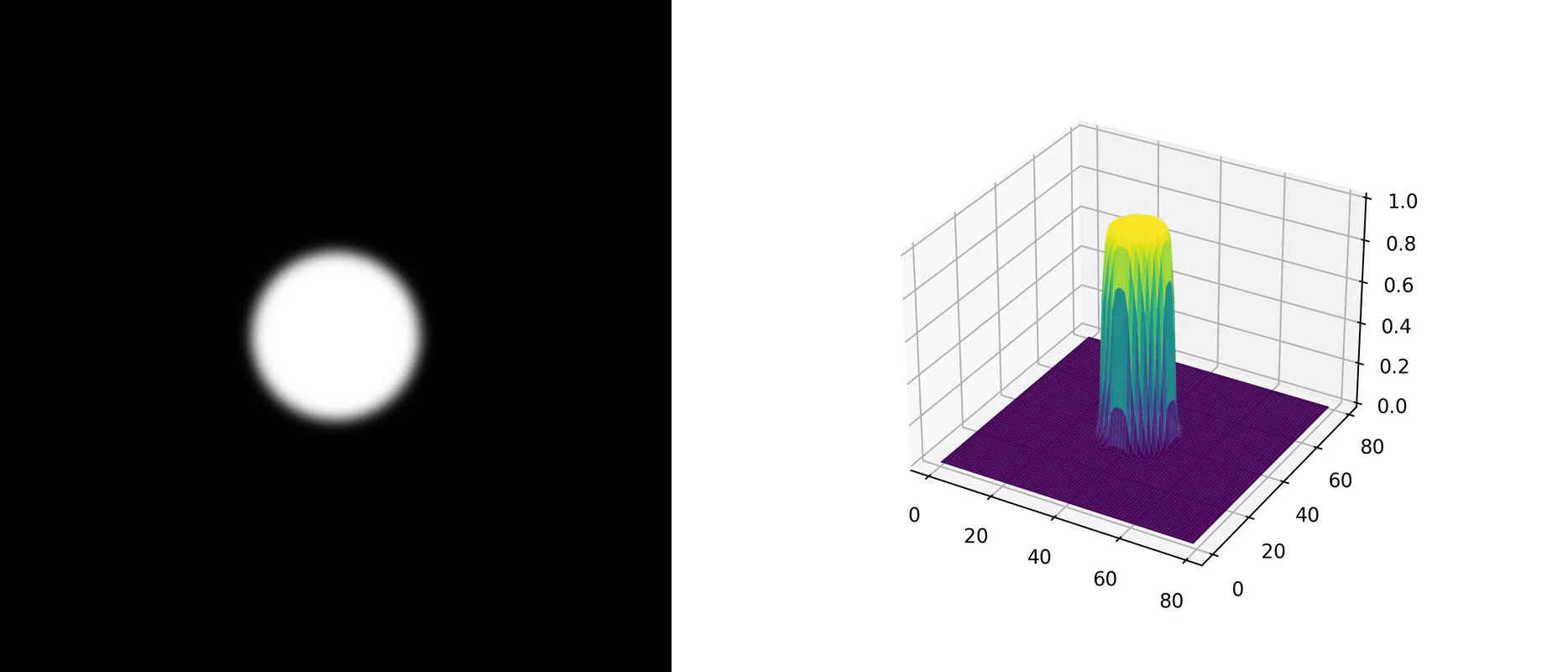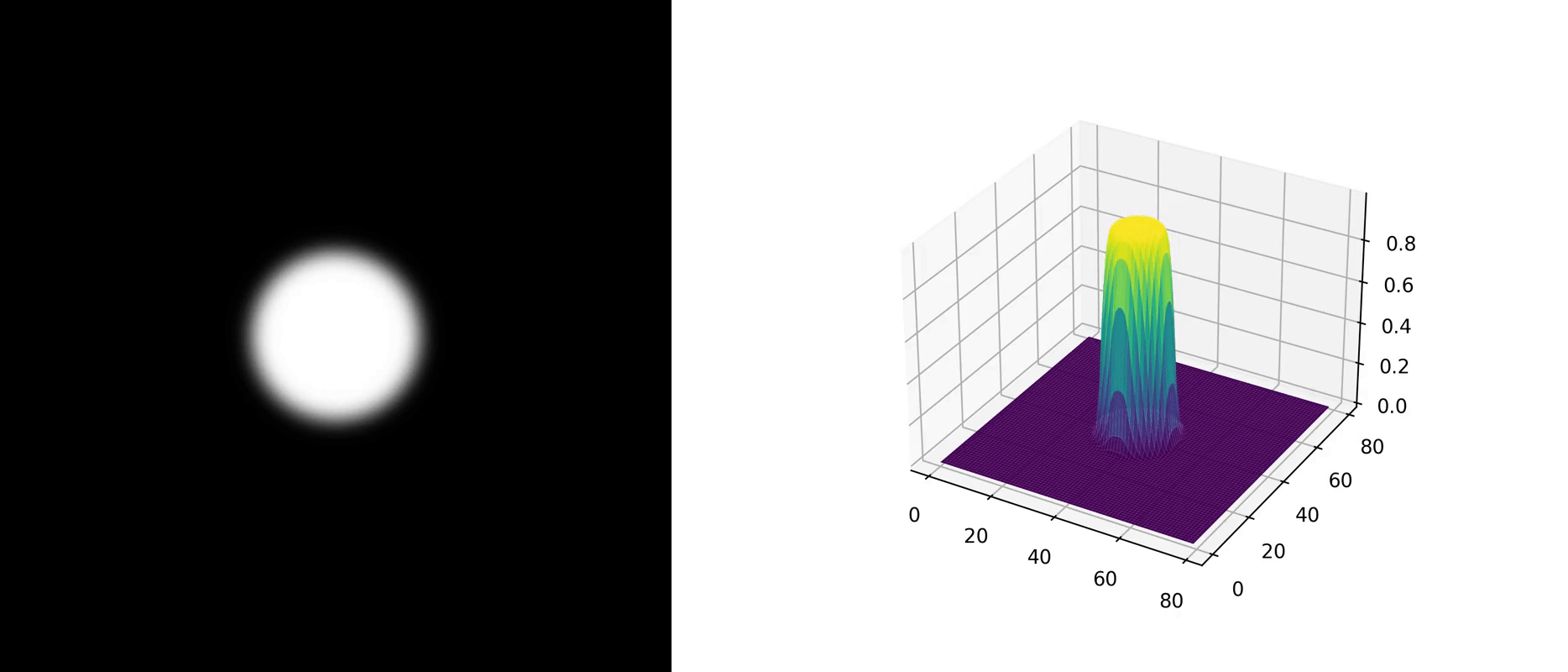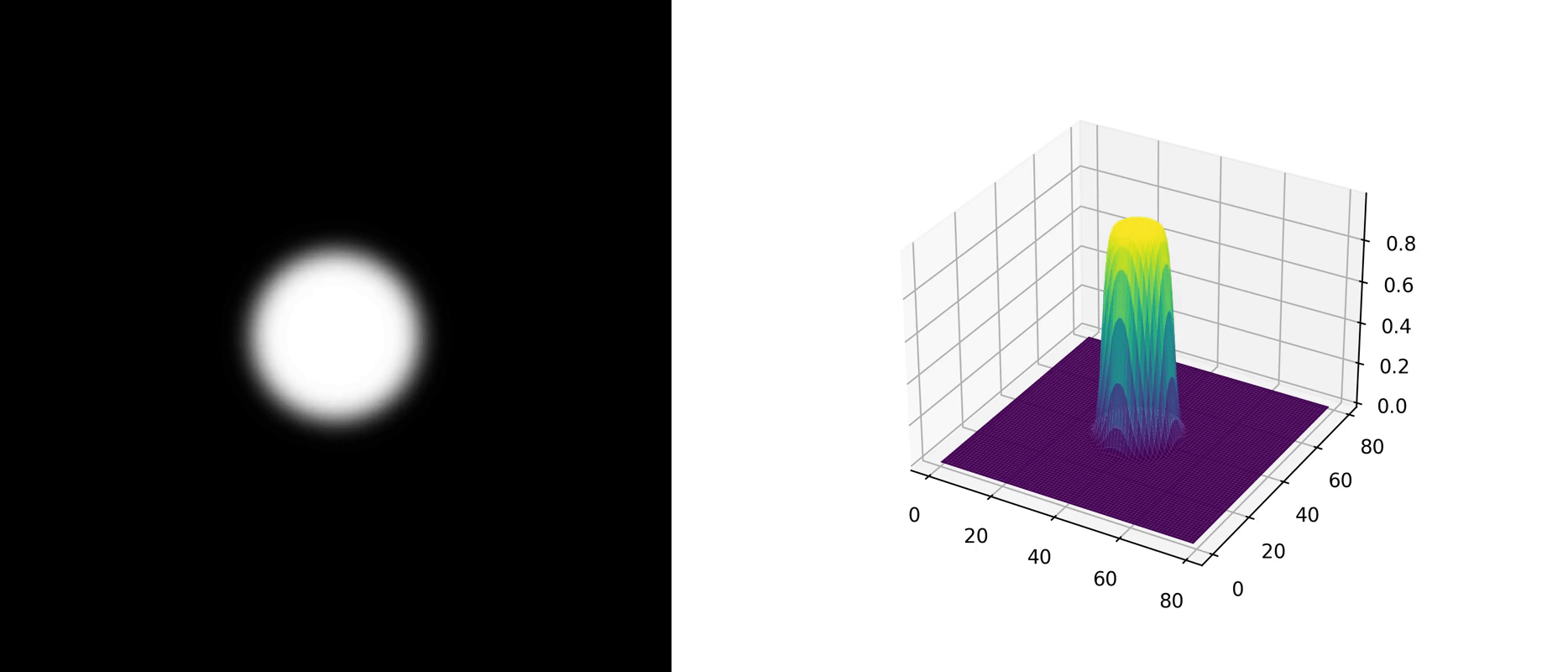
Physical Interpretation

In physical processes, $\alpha$ represents thermal diffusivity, impacting the stability of numerical methods. Its value must be positive. Two questions are left for readers: How would the stability of the numerical method be affected if $\alpha$ were negative? What is the physical interpretation of a negative $\alpha$ ?

Wave Equation

The wave equation's initial value problem is given by $$ \\ \begin{cases} u_{tt} - c^2 \nabla^2 u = 0 & \text{in} \ R^n \times (0, \infty)\\ u = g, \ \ u_t = h &\text{on} \ R^n \times \{t=0\} \end{cases} $$

Exact Solution

As with previous equations, the exact solution’s form is omitted due to its complexity.

Numerical Solution

Using central difference schemes in both time and space, we obtain $$ \frac{u^{n+1}_{i, j} - 2u^n_{i, j} + u^{n-1}_{i, j}}{\Delta t^2} - c^2 \frac{u^n_{i+1, j} + u^n_{i-1, j} + u^n_{i, j+1} + u^n_{i, j-1} - 4u^n_{i, j}}{\Delta x^2} = 0 $$

Stability Analysis

This numerical method is conditionally stable. In two dimensions, the stability condition is $\Delta t < \frac{\Delta x}{c}$. The detailed analysis can be found here.

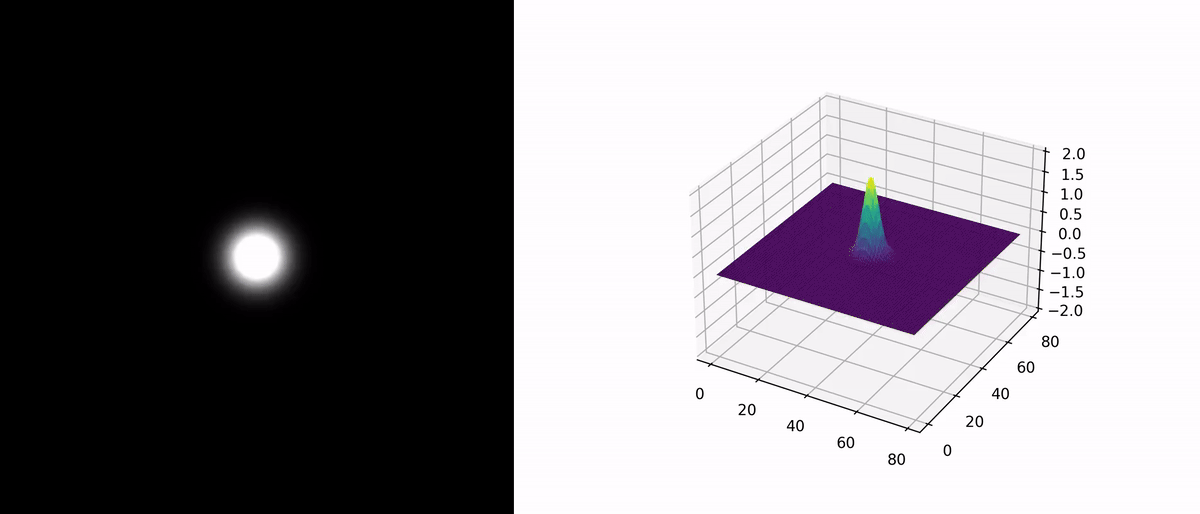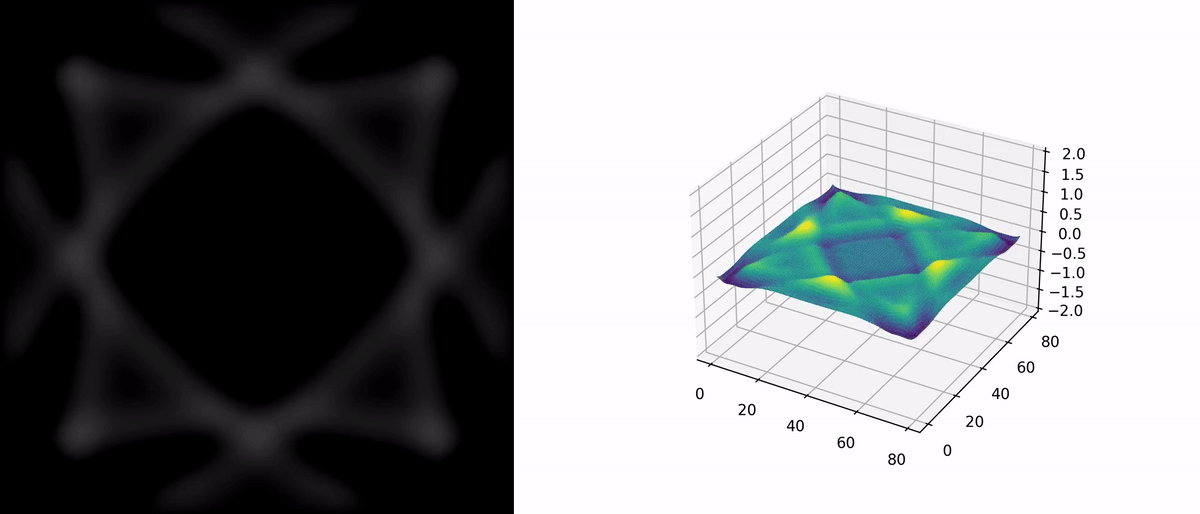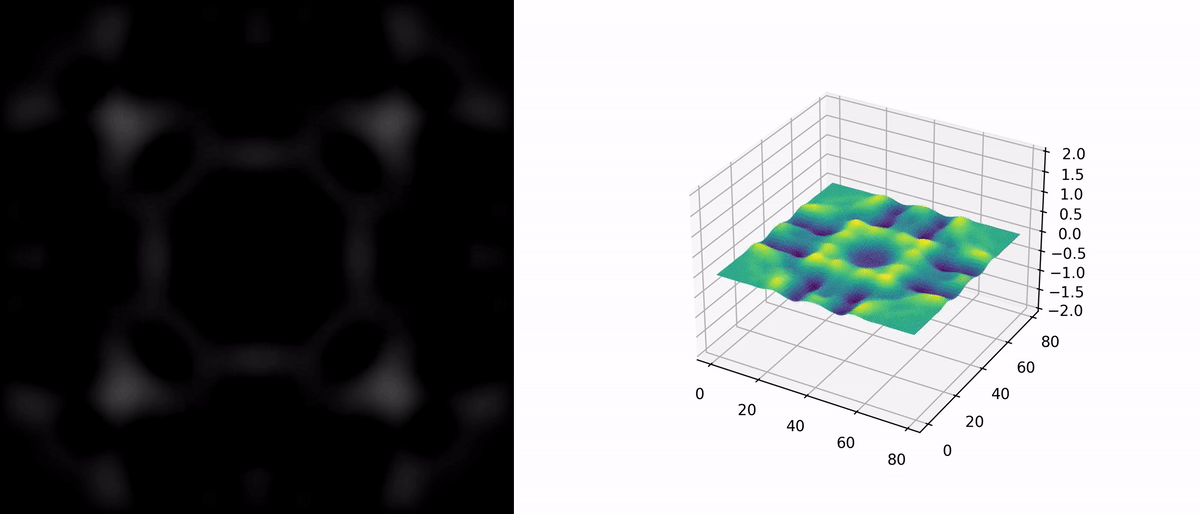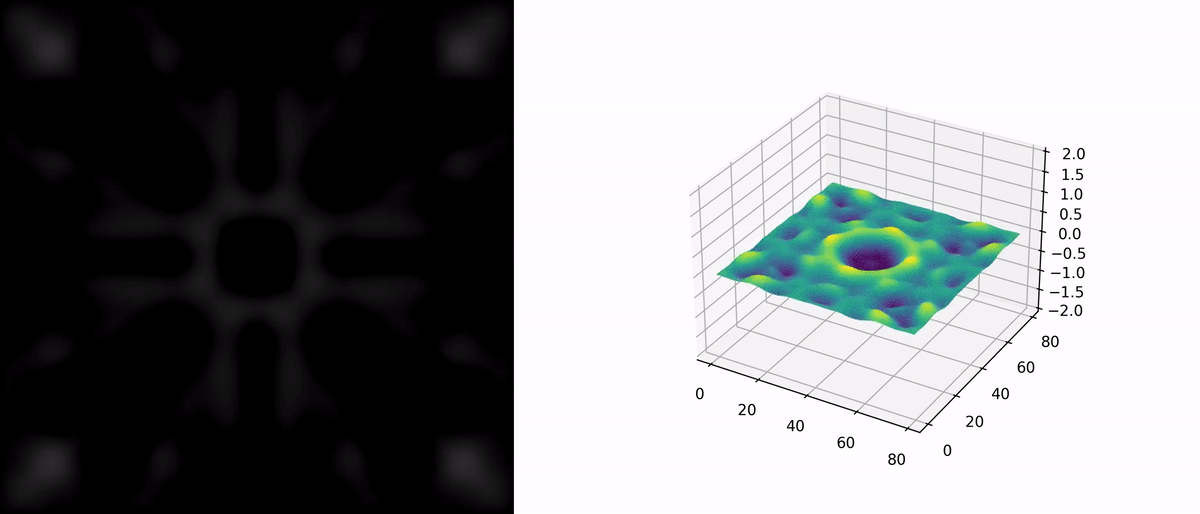
Case Study

A two-dimensional example is provided with the following parameters: $$ \begin{aligned} &c = 1,\\ &g(\mathbf{x}) = 2 e^{-\left(\frac{\mathbf{x}_1^2 + \mathbf{x}_2^2}{16}\right)} \end{aligned} \\ $$ Boundary conditions for the simulation region are set as fixed boundaries.

As there is no direct comparison case, we do not show the visualization of the exact solution. The figure below illustrates the numerical solution’s evolution over time.

Code